一. 线性代数与群表示理论基础
【定义 1.1】(线性空间)
数域
【定义 1.2】(线性无关与维数)
线性空间
【定义 1.3】(基矢)
设
【定义 1.4】(线性变换)
线性变换
【定义 1.5】(线性变换群)
定义两个变换的乘法为两个线性变换的相继作用(即矩阵乘法),则
【定义 1.6】(群表示)
设有群
【定义 1.7】(等价表示)
设群
【定义 1.8】(不可约表示)
设
【定义 1.9】(线性空间的直和)
设线性空间
二. 总体思路
【定理 2.1】(勃恩赛德(Burnside)定理)有限群的所有不等价不可约表示维数的平方和等于群的阶,即:
这个等式说明了将一个群写为其所有不等价不可约表示的矩阵形式时数据量仍是
【定义 2.2】(有限群傅里叶变换)
函数
其逆变换为
可以看出傅里叶变换
和通常一样,这种变换可以将卷积化为点乘:
其中卷积定义为
其中
使得
综上所述,当表示空间基底合适时,所有的
三. 对称群 S_n 的不可约表示
对称群
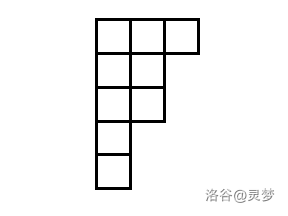
如在第 2 节中描述的,我们在算法中使用一系列嵌套子群
其中
换句话说,
我们取
另一方面,分支定理说明了
【定理 3.1】(分支定理(Branching theorem))
令
举个例子,令
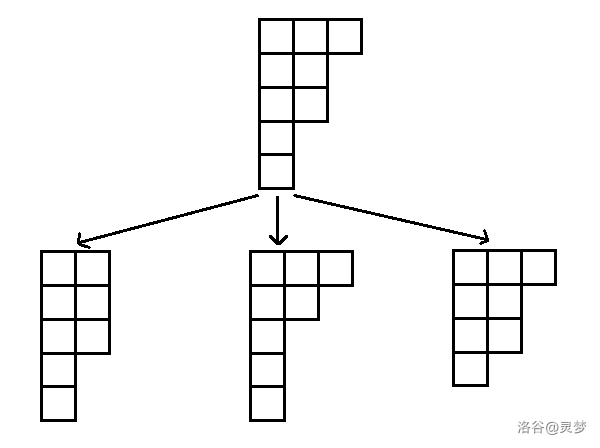
这意味着对于
至于整数划分如何对应对称群的不可约表示,以及取什么样的基底能使
四. 杨氏半正规表示
将正整数
【定义 4.1】(末标号序)
标准杨表的末标号序(last letter order)一种线性序,其定义如下:考虑两个相同形状的
【定义 4.2】(轴向距离)
对于一张杨表(不一定是标准的)
如果认为往左下走的贡献为正,往右上走的贡献为负,容易发现这是
【定义 4.3】(杨氏半正规表示)
固定一个划分
- 矩阵的维数即为
\lambda 所对杨表的个数,行和列的标号从1 开始; - 对于主对角线上的元素,有
(\rho_\lambda((t,t+1)))_{i,i}=d^i(t,t+1)^{-1} ; - 对于末标号序第
i 的标准杨表,若它交换标号t 与t+1 的位置后得到的杨表仍是标准的,设这张表的末标号序为j ,则(\rho_\lambda((t,t+1)))_{i,j}=\left\{\begin{matrix}1-d^i(t,t+1)^{-2}&i<j\\1&i>j\end{matrix}\right.. - 其他未赋值的位置元素值为
0 。
现在我们得到了所有交换相邻元素的置换在
除了杨氏半正规表示,还有杨氏正交表示等其他常用基矢,也拥有各种性质,这里不做详细介绍。
五. 实现 & 复杂度分析
下面是对称群上的快速傅里叶变换的一个简单实现。我借鉴了资料 4(SnOB)的写法,删掉了一些不必要的类,并采用迭代法(资料 2 的算法 5)降低空间复杂度。采用编译器标准为 ISO C++11。
1. 类的定义
首先定义一个矩阵类,封装矩阵的基本运算。然后再定义对称群不可约表示类,这里采用了杨氏半正规表示,需要在接下来的预处理过程中完成计算。applyCycle() 用于左乘一个循环移位置换,使用 tdash,dist 两个数组可以在不用构建矩阵的情况下算出贡献。
const int MaxN=11;
// 矩阵类
struct Matrix {
int dim;
double* A;
// 生成一个 n*n 的方阵
Matrix(int n): dim(n) { A = new double[n*n](); }
// 复制矩阵 o
Matrix(const Matrix& o) : dim(o.dim) {
A = new double[dim*dim];
for (int i=0; i<dim*dim; i++) A[i] = o.A[i];
}
// 构建 mlist 组成的分块矩阵
Matrix(int n, const vector<Matrix*>& mlist): dim(n) {
A = new double[n*n]();
int t = 0;
for (Matrix* mat: mlist) {
for (int i=0; i<mat->dim; i++)
for (int j=0; j<mat->dim; j++)
at(i+t, j+t) = mat->at(i, j);
t += mat->dim;
}
}
// 获取矩阵第 i 行第 j 列的元素
double& at(int i, int j) const { return A[i*dim+j]; }
// 矩阵乘法(O(n^3))
Matrix* operator * (const Matrix& o) const {
Matrix* res = new Matrix(dim);
for (int i=0; i<dim; i++)
for (int k=0; k<dim; k++)
for (int j=0; j<dim; j++)
res->at(i, j) += at(i, k)*o.at(k, j);
return res;
}
// 累加矩阵 o
void operator += (const Matrix& o) {
for (int i=0; i<dim*dim; i++) A[i] += o.A[i];
}
// 打印矩阵,调试用
void print() {
for (int i=0; i<dim; i++) {
for (int j=0; j<dim; j++)
printf("%lf ", at(i, j));
putchar('\n');
}
}
};
// 对称群不可约表示类(Irreducible Representations)
struct Irrep {
vector<int> part; // 对应的划分,part[i] 表示第 i 行的格子数
int deg; // 表示的维数
vector<int> eta; // 由分支定理拆分得到的 S_(n-1) 群表示编号
int* tdash[MaxN]; // tdash[t][i] 为第 i 张杨表交换标号 t,t+1 得到的杨表的末标号序,得到的不是标准杨表则取 -1
int* dist[MaxN]; // dist[t][i] 为第 i 张杨表上标号 t 到 t+1 的轴向距离
Irrep(const vector<int>& p):
part(p), deg(0) { eta.clear(); }
// 将矩阵 M 左乘置换 [[p,q]] 上的表示矩阵,若 inv 为真则是左乘逆矩阵
void applyCycle(Matrix& M, int p, int q, bool inv) const {
bool done[deg];
for (int l=q-1; l>=p; l--) {
int t = inv ? p+q-1-l: l;
for (int i=0; i<deg; i++) done[i]=0;
for (int i=0; i<deg; i++) if (!done[i]) {
int j = tdash[t][i];
double c1 = 1.0/dist[t][i];
if (j==-1) {
for (int k=0; k<deg; k++) M.at(i, k) *= c1;
} else {
double c2 = 1-c1*c1;
for (int k=0; k<deg; k++) {
double tmp = M.at(i, k);
M.at(i, k) = c1*tmp+c2*M.at(j, k);
M.at(j, k) = -c1*M.at(j, k)+tmp;
}
done[j] = 1;
}
}
}
}
};
int order[MaxN]; // 群 S_n 的阶数(即 n!)
vector<Irrep> R[MaxN]; // S_n 的所有不可约表示
int* rev[MaxN]; // 迭代实现 FFT 需要预处理的数组,rev[i] 为字典序排名为 i 的排列倒置后的字典序2. 预处理
预处理部分主要是完成对 Irrep 类以及 rev 数组的计算。这一部分的实现比较精细,使用了一些技巧来降低编码难度(比如不需要存储杨表),但代价是可读性稍差了一些。具体细节请结合注释理解。
void prework(int N) {
// 直接写出 n=0,1 的情况
R[0].push_back(Irrep(vector<int>()));
R[0][0].deg = 1;
R[1].push_back(Irrep(vector<int>({1})));
R[1][0].deg = 1;
R[1][0].eta.push_back(0);
order[1] = 1;
rev[1] = new int[1]();
vector<int> lst({1}); // 这里的 lst[i] 为字典序第 i 的排列的最后一个元素,计算 rev 时要用到
for (int n=2; n<=N; n++) {
// 由 S_(n-1) 的表示推出 S_n 的表示,保证按划分的字典序递增排列
for (const Irrep& lambda: R[n-1]) {
vector<int> p = lambda.part;
p.push_back(1);
R[n].push_back(Irrep(p));
p.pop_back();
if (p.size()==1 || p[p.size()-1]<p[p.size()-2]) {
p[p.size()-1]++;
R[n].push_back(Irrep(p));
}
}
int pos[R[n-2].size()];
for (Irrep& lambda: R[n]) {
vector<int> p = lambda.part;
// 计算分支的编号 eta
for (int i=0, j=0; i<p.size(); i++) {
if (i==p.size()-1 || p[i]>p[i+1]) {
if (--p[i]==0) p.pop_back();
while (R[n-1][j].part!=p) j++;
lambda.deg += R[n-1][j].deg;
lambda.eta.push_back(j);
if (i==p.size()) p.push_back(0);
p[i]++;
}
}
for (int i=1; i<n; i++) {
lambda.tdash[i] = new int[lambda.deg];
lambda.dist[i] = new int[lambda.deg];
for (int j=0; j<lambda.deg; j++) lambda.tdash[i][j]=-1;
}
for (int i=0; i<R[n-2].size(); i++) pos[i]=-1;
// 计算 tdash
// 原理为依次删去杨图中标号为 n,n-1 的两个格子,若两种顺序不同的删法得到了同样的杨图,那么这两组杨表可以对应交换标号 n-1,n 互相得到
// 第一次删格子得到某个杨图时在 pos 上做记录,第二次就可以直接找到这张杨图的编号了
int t = 0;
for (int i: lambda.eta) {
for (int j=1; j<n-1; j++) {
for (int k=0; k<R[n-1][i].deg; k++) {
if (~R[n-1][i].tdash[j][k])
lambda.tdash[j][k+t] = R[n-1][i].tdash[j][k]+t;
lambda.dist[j][k+t] = R[n-1][i].dist[j][k];
}
}
for (int j: R[n-1][i].eta) {
if (~pos[j]) {
for (int k=0; k<R[n-2][j].deg; k++) {
lambda.tdash[n-1][t+k] = pos[j]+k;
lambda.tdash[n-1][pos[j]+k] = t+k;
}
}
pos[j] = t; // 不能加 else,否则计算 dist 时会出错
t += R[n-2][j].deg;
}
}
// 计算 dist
// 二次利用 pos 数组,pos[i] 此时记录了删去两个格子得到了 S_(n-2) 中编号 i 杨图的 n 阶杨图,且是末标号较大的一者
// 根据这一关系可以得出两组杨表中标号 n-1,n 分别所在的位置,进一步得出 dist. 注意处理 n-1,n 在同一行的情况
for (int i=0; i<R[n-2].size(); i++) {
if (~pos[i]) {
int a=-1, b=-1;
for (int j=0; j<p.size(); j++)
if (j>=R[n-2][i].part.size() || p[j]>R[n-2][i].part[j])
if (a==-1) a=j; else b=j;
int d = ~b ? p[a]-p[b]+b-a : -1;
int tdash = lambda.tdash[n-1][pos[i]];
for (int j=0; j<R[n-2][i].deg; j++) {
lambda.dist[n-1][pos[i]+j] = d;
if (~tdash) lambda.dist[n-1][tdash+j] = -d;
}
}
}
}
order[n] = order[n-1]*n;
// 由 S_(n-1) 的 lst,rev 推出 S_n 的
rev[n] = new int[order[n]];
lst.resize(order[n]);
for (int i=0; i<order[n-1]; i++) lst[i]++;
for (int i=2; i<=n; i++)
for (int j=(i-1)*order[n-1]; j<i*order[n-1]; j++) {
lst[j] = lst[j-order[n-1]];
if (lst[j]==i) lst[j]--;
}
int q[MaxN]={0};
for (int i=0; i<order[n]; i++)
rev[n][i] = (lst[i]-1)*order[n-1]+rev[n-1][q[lst[i]]++];
}
}3. S_n 快速傅里叶变换
对数组 a 做傅里叶变换,返回的是一系列矩阵的指针。采用了迭代的思想,实现方法上文已有描述。
vector<Matrix*> FFT(double* a, int N) {
vector<Matrix*> f(order[N]), g;
for (int i=0; i<order[N]; i++) {
f[i] = new Matrix(1);
f[i]->at(0, 0) = a[rev[N][i]];
}
for (int n=2; n<=N; n++) {
g.resize(order[N]/order[n]*R[n].size());
for (int p=0; p<order[N]/order[n]; p++) {
for (int i=0; i<R[n].size(); i++) {
const Irrep& lambda = R[n][i];
g[p*R[n].size()+i] = new Matrix(lambda.deg);
for (int k=1; k<=n; k++) {
vector<Matrix*> branches;
for (int j: lambda.eta)
branches.push_back(f[(p*n+k-1)*R[n-1].size()+j]);
Matrix M(lambda.deg, branches);
lambda.applyCycle(M, k, n, 0);
(*g[p*R[n].size()+i]) += M;
}
}
}
swap(f, g);
for (Matrix* mat: g) delete mat;
}
return f;
}4. S_n 快速傅里叶逆变换
可以当作是傅里叶变换的逆过程,而不需要按
double* iFFT(vector<Matrix*> f, int N) {
vector<Matrix*> g;
for (int i=0; i<R[N].size(); i++)
f[i] = new Matrix(*f[i]);
for (int n=N; n>=2; n--) {
g.resize(order[N]/order[n-1]*R[n-1].size());
for (int p=0; p<order[N]/order[n]; p++) {
for (int k=1; k<=n; k++) {
for (int j=0; j<R[n-1].size(); j++)
g[(p*n+k-1)*R[n-1].size()+j] = new Matrix(R[n-1][j].deg);
for (int i=0; i<R[n].size(); i++) {
const Irrep& lambda = R[n][i];
Matrix M = *f[p*R[n].size()+i];
lambda.applyCycle(M, k, n, 1);
int c = 0;
for (int j: lambda.eta) {
Matrix* Msubset = g[(p*n+k-1)*R[n-1].size()+j];
int deg = R[n-1][j].deg;
double mult = (double)lambda.deg/(n*deg);
for (int a=0; a<deg; a++)
for (int b=0; b<deg; b++)
Msubset->at(a, b) += M.at(c+a, c+b)*mult;
c += deg;
}
}
}
}
swap(f, g);
for (Matrix* mat: g) delete mat;
}
double* a = new double[order[N]];
for (int i=0; i<order[N]; i++)
{
a[rev[N][i]] = f[i]->at(0, 0);
delete f[i];
}
return a;
}此外,模质数剩余系下的实现也很容易由上面的代码修改得到,不再赘述。
5. 复杂度分析
无法分析.jpg
取矩阵乘法的复杂度为
 冷滟泽的个人博客
冷滟泽的个人博客